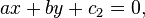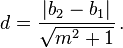점과 직선 사이의 거리

위키피디아 http://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line

A geometric proof[edit]

Diagram for geometric proof

This proof is valid only if the line is not horizontal or vertical.^[4]

Drop a perpendicular from the point P with coordinates (x₀, y₀) to the line with equation Ax + By + C = 0. Label the foot of the perpendicular R. Draw the vertical line through P and label its intersection with the given line S. At any point T on the line, draw a right triangle TVU whose sides are horizontal and vertical line segments with hypotenuse TU on the given line and horizontal side of length |B| (see diagram). The vertical side of ∆TVU will have length |A| since the line has slope -A/B.

∆SRP and ∆TVU are similar triangles since they are both right triangles and ∠PSR ≅ ∠VUT since they are corresponding angles of a transversal to the parallel lines PS and UV (both are vertical lines).^[5] Corresponding sides of these triangles are in the same ratio, so:

If point S has coordinates (x₀,m) then |PS| = |y₀ - m| and the distance from P to the line is:

Since S is on the line, we can find the value of m,

and finally obtain:^[6]

A vector projection proof[edit]

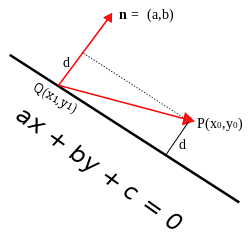
Let P be the point with coordinates (x₀, y₀) and let the given line have equation ax + by + c = 0. Also, let Q = (x₁, y₁) be any point on this line and n the vector (a, b) starting at point Q. The vector n is perpendicular to the line, and the distance d from point P to the line is equal to the length of the orthogonal projection of  on n. The length of this projection is given by:

Now,

 so  and 

thus

Since Q is a point on the line, , and so,^[7]

---

두 직선 사이의 거리

When the lines are given by

the distance between them can be expressed as

---

점과 평면 사이의 거리

수학의 정석 - 기하와 벡터

수학의 샘 - 기하와 벡터

풍산자 - 기하와 벡터